|
Facciamo un breve cenno sulle coordinate polari nello spazio 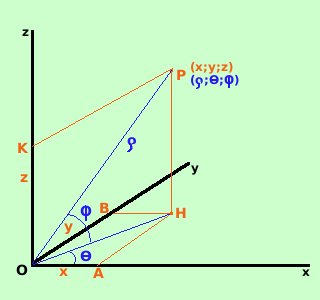 Considero Il sistema cartesiano ortogonale Oxyz e considero il punto
P di coordinate (x;y;z)
Considero Il sistema cartesiano ortogonale Oxyz e considero il punto
P di coordinate (x;y;z) Ho: OK = z OA = x OB = y Congiungo il punto P con l'origine degli assi O ed ottengo PO = Considero ora il triangolo rettangolo POH in esso avremo valide le relazioni: z = OK = PH = OH = e quindi per trovare x ed y, considerando il triangolo rattangolo OHA: x = OA = OH sen y = AB = AH = OH cos Quindi avremo le tre formule di trasformazione da coordinate cartesiane a coordinate polari
Viceversa avremo per le trasformazioni da coordinate polari a coordinate cartesiane
|

|

|

|

|