Nota con un po' di filosofia Veramente il fatto di avere un intorno di infinito che si stringe e' una cosa che rende piuttosto perplessi: infatti se considero il punto di vista del punto infinito cosa significa che il suo intorno si stringe? in effetti non significa nulla: un intorno infinito resta sempre un intorno infinito per quanto io cerchi di stringerlo. Anche dal punto di vista dell'intervallo abbiamo dei problemi: come puo' stringersi un intervallo che contenga l'infinito? L'unica cosa che possiamo vedere e' che il bordo dell' intorno o il bordo dell'intervallo si allontana da un qualunque punto prefissato di quantita' sempre maggiori; cioe' il concetto di limite infinito non e' una cosa oggettiva ma una cosa dipendente dall'osservatore; Le scuole matematiche sono sempre state due, quelle che io chiamo i pitagorici e gli aristotelici: i pitagorici pensano che la matematica sia la realta', gli aristotelici invece pensano che la matematica sia una costruzione umana e che abbia riscontro nella realta' in quanto la realta' stessa viene filtrata attraverso il nostro cervello: Il concetto di limite infinito e' una concezione non accettabile per i pitagorici ma in linea con il pensiero matematico aristotelico In pratica, siccome la matematica ci serve, la costruiamo sulla nostra misura, quindi anche il concetto di infinito, anche se non e' il concetto oggettivo di infinito, e' un concetto che per noi e per i nostri bisogni e' piu' che sufficiente, anche se, secondo me, e' piuttosto riduttivo. Per vederne l'equivalente geometrico pensate una retta ed un punto fuori di essa, se dal punto traccio 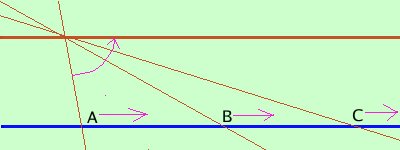una retta obliqua questa incontrera' la prima retta in un punto A, se ora ruoto la retta, fino a farla diventare parallela, il punto si spostera' fino all'infinito e quando la retta sara' parallela il punto sparira', ma non appena ruotero' la retta anche di un millesimo di grado il punto ricomparira' dall'altra parte; Questo ragionamento e' valido finche' io sto al finito a guardare cosa succede. Quindi mettendoci sul punto di vista del finito considereremo ad esempio una retta come una circonferenza di raggio infinito in cui l'infinito (senza segno) e' un punto ed invece in analisi considereremo l'infinito talvolta un punto solo e quindi senza segno(oppure con ±∞) e talvolta come due punti uno col segno positivo ed uno col segno negativo