|
Quando scrivero' log x intendero' ln x cioe' il logaritmo naturale di x Determinare i punti di massimo e minimo per la seguente funzione nell'intervallo a fianco segnato x y = ------ 0 log x La prima cosa da dire e' che l'intervallo esatto e' 0 < x perche' log x non e' definito per x=0 e il denominatore della funzione si annulla per x=1 Trovo la derivata prima e la pongo uguale a zero log x - 1 y' = ------------ log2 x log x - 1 = 0 log x = 1 x = e Trovo il valore della y corrispondente sostituendo e al posto di x nell'equazione di partenza e y(e)= -------- = e log e Il punto estremante e' A(e , e) siccome io devo considerare i valori della funzione all'interno dell'intervallo 0 < x C'e' anche da dire che non appartenendo lo zero all'intervallo di definizione in zero non avro' ne' massimo ne' minimo se non come limite Nel punto 0 dovro' fare il limite destro mentre nel punto 2 trovo il valore dellea y corrispondente sostituendo 2 al posto di x nell'equazione di partenza, infine nel punto 1 calcolero' il limte della funzione
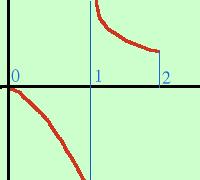 Anche se per avere una visione corretta dovresti aver fatto gli asintoti, comunque un grafico molto intuitivo potrebbe essere quello che vedi qui a fianco |