|
Trovare le equazioni degli asintoti per la funzione ex y = ---------- log x il campo di esistenza e' l'insieme dei valori in cui e' definita la funzione logaritmo (x>0) togliendo inoltre il valore x=1 per cui si annulla il denominatore C.E. = ] 0 , 1[ U ] 1 , + calcolo il limite nell'estremo del campo di esistenza:
Calcolo ora il limite nel punto di discontinuita'
x = 1 e' un asintoto verticale Per tracciare al meglio l'andamento della funzione vicino all'asintoto calcoliamo il limite destro e sinistro della funzione nel punto di ascissa 1 limite sinistro:
limite destro:
per calcolare limiti di questo genere basta ricordare che ex e' sempre positiva mentre il logaritmo e' negativo per x minore di 1 ed e' positivo per x maggiore di 1, bisogna poi fare il conto dei segni 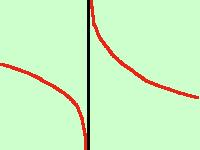 quindi il risultato e' quello della figura a destra
quindi il risultato e' quello della figura a destraPer quanto riguarda l'asintoto orizzontale od obliquo facciamo il limite per x tendente a piu' infinito della funzione (solo piu' infinito perche' per valori inferiori a zero la funzione non esiste)
questo limite e' particolarmente semplice calcolato con la regola di De l'Hôpital puo' esistere l'asintoto obliquo nella forma y = mx + q, naturalmente se esistono m e q vediamo se esiste m moltiplicando il denominatore per x
Non abbiamo asintoti orizzontali ne' obliqui |