|
Trovare le equazioni degli asintoti per la funzione log x y = ---------- ex il campo di esistenza e' l'insieme dei valori in cui e' definita la funzione logaritmo (x>0) C.E. = ] 0, + calcolo il limite nell'estremo del campo di esistenza:
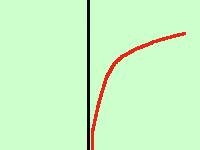 abbiamo che la retta x = 0 e' un'asintoto verticale e la funzione inizia da -
abbiamo che la retta x = 0 e' un'asintoto verticale e la funzione inizia da -Per quanto riguarda l'asintoto orizzontale od obliquo facciamo il limite per x tendente a piu' infinito della funzione (solo piu' infinito perche' per valori inferiori a zero la funzione non esiste)
Per calcolare questo limite con il confronto di infiniti basta ricordare che ex e' l'infinito di ordine superiore a tutti gli altri Abbiamo quindi l'asintoto orizzontale che coincide con l'asse delle x y = 0 |