|
Data l'equazione di una retta e l'equazione di una circonferenza, se le due curve hanno dei punti in comune deve essere possibile trovarne le coordinate perche' geometricamente possiamo trovare i punti comuni. I punti comuni appartengono contemporaneamente alla retta ed alla circonferenza, quindi bastera' imporre che l'equazione della retta e l'equazione della circonfernza valgano contemporaneamente, cio' equivale a fare il sistema fra le due equazioni. Le coordinate dei punti che si trovano contemporaneamente sulla retta e sulla circonferenza saranno le soluzioni del sistema Vediamo un esercizio Trovare i punti comuni alla retta y = -2x + 6 ed alla circonferenza 2x2+ 2y2 - 6x - 7y = 0 Possiamo dire subito che la circonferenza passa per l'origine perche' manca il termine noto c Inoltre e' sempre consigliabile fare la rappresentazione geometrica per poter controllare se i risultati sono accettabili Imposto il sistema 2x2+ 2y2 - 6x - 7y = 0 sostituisco 2x2+ 2(-2x + 6)2 - 6x - 7(-2x + 6) = 0 Eseguo i calcoli 2x2+ 2(4x2 - 24x + 36) - 6x + 14x - 42 = 0 2x2+ 8x2 - 48x + 72 - 6x + 14x - 42 = 0 10x2+ - 40x + 30 = 0 Divido tutto per 10 (cosi' semplifico i calcoli) x2+ - 4x + 3 = 0 applico la formula risolutiva per l'equazione di secondo grado -(-4) x1,2 = ---------------------------------- 2(1) eseguo i calcoli 4 x1,2 = ------------------ 2 4 x1,2 = ---------------- 2 4 x1,2 = ---------- 2 Otteniamo le due soluzioni x1 = (4+2)/2 = 6/2 = 3 x2 = (4-2)/2 = 2/2 = 1 Sostituisco la prima soluzione nel sistema x = 3 x = 3 x = 3 Primo punto di intersezioneA(3,0) Sostituisco la seconda soluzione nel sistema x = 1 x = 1 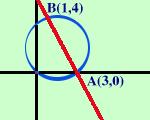
x = 1 Secondo punto di intersezioneB(1,4) A destra la rappresentazione grafica |

|

|

|

|