|
L'ellisse si otteneva come somma; l'iperbole si ottiene come differenza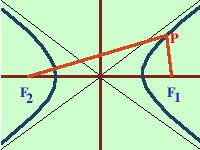 
L'iperbole e' il luogo geometrico dei punti del piano per cui e' costante la differenza delle distanze da due punti fissi detti fuochi
Significa che per tutti i punti P della figura avremo che PF2 - PF1 = costante Per sapere quanto vale la costante spostiamo il punto P fino a portarlo sull'asse orizzontale, allora si vede che la differenza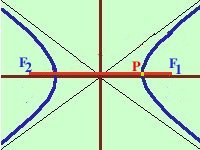 
PF2 - PF1
e' uguale alla distanza fra i due punti dell'iperbole che tagliano l'asse delle x (asse orizzontale). Chiamiamo questa distanza 2a (a per indicare che e' una costante e 2 perche', essendo l'iperbole simmetrica spesso ci servira' la meta' della distanza, cioe' il semiasse orizzontale); quindi avremo per tutte le iperboli PF2 - PF1 = 2a con a semiasse orizzontale |
|
|
|
|