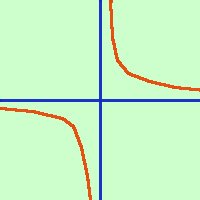
Presa l'equazione dell'iperbole equilatera se operiamo una rotazione di assi
di 45° avremo che gli asintoti corrisponderanno agli assi cartesiani
ortogonali ed otterremo l'equazione
xy = k Per la dimostrazione Questa curva e' importantissima perche' rappresenta la proporzionalita' inversa: cioe' mantenendo k costante se raddoppio la x ottengo che si dimezza la y e se prendo la x cinque volte piu' grande la y si riduce ad un quinto. Tra le applicazioni la piu' intuitiva e' la rappresentazione del legame fra i lati dei rettangoli aventi la stessa area In fisica l'applicazione piu' appariscente e' nella legge delle isoterme PV = nRT in cui le variabili sono P e V mentre nRT corrisponde alla k |
|
|
|
|