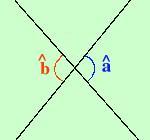
Teorema sugli angoli opposti al vertice Due angoli si dicono opposti al vertice se i lati dell'uno sono sui prolungamneti dei lati dell'altro. In figura gli angoli opposti al vertice sono l'angolo a e l'angolo b Vediamo ora di dimostrare il primo teorema: Due angoli opposti al vertice sono uguali Quando si ha un teorema conviene sempre mettere l'enunciato nella forma se... allora... Se due angoli sono opposti al vertice allora i due angoli sono uguali Dopo il se c'e' l'ipotesi, cioe' quello che sappiamo, dopo l'allora c'e' la tesi, cioe' quello che dobbiamo dimostrare. Ogni volta che dobbiamo dimostrare un teorema conviene costruire una figura e scrivere in modo geometrico l'ipotesi e la tesi Talvolta invece di Ipotesi si scrive Hp (Hypothesis) ed invece di tesi si scrive Th (thesis) perche' fino al 1900 la lingua ufficiale della scienza e quindi della matematica era il latino prima che prendesse il sopravvento la lingua inglese 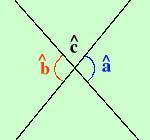Ipotesi ^ ^ a e b opposti al vertice Tesi ^ a = ^ b d'ora in poi tolgo il segno di angolo per poter scrivere in modo piu' compatto, quindi indichero' l'angolo a semplicemente con a senza il simbolo sopra So che a e b sono opposti al vertice. Se sommo l'angolo a con l'angolo c ottengo un angolo piatto a + c = angolo piatto anche se sommo l'angolo b con l'angolo c ottengo un angolo piatto b + c = angolo piatto so che gli angoli piatti (semipiani) sono tutti uguali fra loro, quindi per uno dei postulati sull'uguaglianza (proprieta' transitiva) posso scrivere a + c = b + c Se da due cose uguali tolgo la stessa cosa ottengo ancora cose uguali, allora tolgo prima e dopo l'uguale la c ed ottengo a = b Come volevamo dimostrare