Secondo criterio di congruenza fra triangoli Due triangoli sono congruenti se hanno congruenti due angoli e il lato compreso Per la dimostrazione mettiamo il problema nella forma se... allora... (quello dopo il se e' l'ipotesi e quello dopo l'allora e' la tesi) Se due triangoli hanno congruenti due angoli e il lato compreso allora i triangoli sono congruenti Scriviamolo in modo geometrico: ipotesi, tesi e figura corrispondente Ipotesi 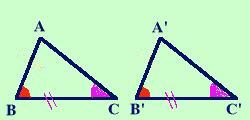BC=B'C' ^ ^ A B C = A' B' C' ^ ^ B C A = B' C' A' tesi ABC=A'B'C' Dimostrazione: Trasporto il lato BC sopra il lato B'C' (posso farlo perche' sono congruenti per ipotesi e potrei farlo in due modi diversi: o traslando il lato o ruotandolo; devo dire che lo porto sopra senza ruotarlo) in modo che l'angolo ABC vada sopra l'angolo A'B'C' e l'angolo BCA vada sopra B'C'A'; in questo modo i due triangoli hanno AB su A'B', BC su B'C' e CA su C'A' quindi sono sovrapposti e coincidono punto per punto come volevamo dimostrare Da notare che per la dimostrazione parto dall'elemento in mezzo agli altri due