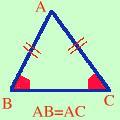
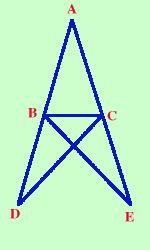
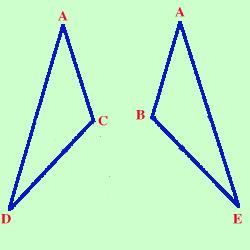
Teorema diretto: Se un triangolo ha due lati congruenti allora ha anche due angoli congruenti Se un triangolo ha due lati congruenti allora ha congruenti anche gli angoli opposti ai lati congruenti Scriviamolo in modo geometrico: ipotesi, tesi e figura corrispondente Ipotesi AB=AC Tesi ^ ^ A B C = B C A Dimostrazione: Nota sulla dimostrazione Prolungo i lati AB ed AC oltre B e C di due segmenti congruenti BD e CE. Ora considero i triangoli ADC ed ABE (per comodita' te li estraggo nella figura a fianco); essi hanno: AB = AC per ipotesi AD = AE perche' somma di segmenti uguali L'angolo in A uguale perche' in comune Quindi i due triangoli sono congruenti per il primo criterio ed in particolare avranno congruenti l'altro lato e gli altri angoli DC=BE    ACD=ABE    ADC=AEB Considero ora i triangoli BDC e BEC; 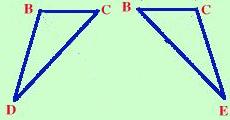essi hanno BD=CE per costruzione (li ho costruiti congruenti) DC=BE perche' appena dimostrato gli angoliBDC=BEC perche' appena dimostrato (corrispondono a ADC=AEB) Quindi i due triangoli sono congruenti per il primo criterio di congruenza ed in particolare avranno gli angoli BCD e CBE congruenti. Ora consideriamo gli angoli ABC ed ACB: essi sono congruenti perche' differenza degli angoli congruenti ACD e ABEcon gli angoli congruenti BCD e CBE ACD - BCD = ACB     ABE - CBE = ABC Come volevamo dimostrare Da notare che per il teorema diretto e' sufficiente usare il primo criterio; infatti quando studiavo io veniva trattato subito dopo il primo criterio di congruenza; poi si e' preferito metterlo dopo il secondo criterio assieme al suo inverso in modo da formare quasi un unico teorema