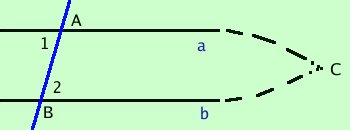
Criterio fondamentale del parallelismo Se due rette tagliate da una trasversale formano angoli alterni interni uguali allora le due rette sono parallele Facciamo la dimostrazione per assurdo Ipotesi angolo 1 = angolo 2             Tesi a // b Dimostrazione: Supponiamo che le rette non siano parallele, cio' significa che, magari dopo qualche chilometro si incontreranno in un punto C (per questo ho messo il tratteggio). Cio' significa che si forma il triangolo CAB ed in questo triangolo l'angolo 1 e' esterno mentre l'angolo 2 e' interno non adiacente, quindi l'angolo 1 deve essere maggiore dell'angolo 2 contro l'ipotesi. Ho negato l'ipotesi quindi il criterio e' vero. D'ora in avanti per mostrare che due rette sono parallele bastera' mostrare che gli angoli alterni interni sono uguali Equivalentemente potrai mostrare anche che sono uguali gli angoli alterni esterni gli angoli corrispondenti sono supplementari (la loro somma e' un angolo piatto) gli angoli coniugati interni gli angoli coniugati esterni