Teorema ogni diagonale divide un parallelogramma in due triangoli congruenti e viceversa Se un quadrilatero e' diviso da ogni diagonale in due triangoli congruenti allora il quadrilatero e' un parallelogramma Dimostriamo prima il teorema diretto e poi il teorema inverso teorema diretto Ogni diagonale divide un parallelogramma in due triangoli congruenti ipotesi AB // CD    BC // AD tesi     ABD = BCD     Dimostrazione (uguale alla prima) congiungo i punti B e D ed ottengo i due triangoli ABD e BDC; essi hanno: 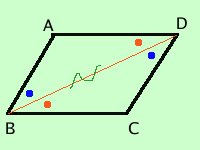l'angolo ABD^ congruente all'angolo BDC^ perche' alterni interni rispetto alle parallele AB e CD tagliate dalla trasversale BD l'angolo ADB^ congruente all'angolo DBC^ perche' alterni interni rispetto alle parallele AD e BC tagliate dalla trasversale BD il lato BD in comune Quindi i due triangoli ABD e BCD sono congruenti per il secondo criterio di congruenza dei triangoli (un lato e due angoli), come volevamo 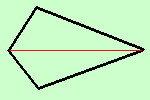teorema inverso da notare che nel teorema specifico "ogni" diagonale perche' altrimenti, nel teorema inverso, potrebbe trattarsi di un "romboide" (tipo aquilone) Se un quadrilatero e' diviso in due triangoli congruenti da entrambe le diagonali allora il quadrilatero e' un parallelogramma ipotesi    ABD = BCD    ABC = ACD tesi AB // CD    BC // AD Dimostrazione I triangoli ABD e BCD sono congruenti per ipotesi e quindi hanno congruenti tutti gli elementi 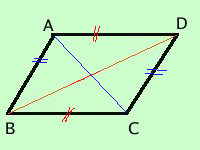Anche i triangoli ABC e ACD sono congruenti per ipotesi e quindi hanno congruenti tutti gli elementi in particolare AB=CD ed AD=BC ma questi essendo lati opposti congruenti di un quadrilatero ne segue che il quadrilatero e' un parallelogramma (come abbiamo gia' dimostrato) Avendo dimostrato sia il teorema diretto che quello inverso i due fatti, parallelogramma e lati opposti congruenti, saranno equivalenti