Circocentro Definiamo circocentro di un triangolo il punto di incontro degli assi dei suoi lati 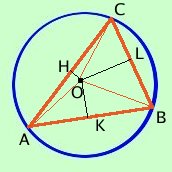Il circocentro e' il centro della circonferenza circoscritta al triangolo Mostriamo che gli assi dei lati di un triangolo passano tutti per lo stesso punto e che tale punto e' il centro della circonferenza circoscritta. Consideriamo l'asse KO del segmento AB e l'asse LO del segmento BC, essi si incontreranno in un punto O: Per definizione di asse del segmento AB avremo AO = BO Per definizione di asse del segmento BC avremo BO = CO Per la proprieta' transitiva della congruenza avremo che AO = CO Quindi per definizione di asse del segmento il punto O e' sull'asse del segmento AC Considerando i tre segmenti congruenti AO, BO, CO come raggi potremo tracciare la circonferenza di centro O circoscritta al triangolo, come volevamo Viceversa, se O e' il centro della circonferenza circoscritta al triangolo ABC essendo OA = OB = OC perche' raggi, avremo che O appartiene agli assi dei segmenti AB, BC ed AC sempre per la definizione di asse di un segmento