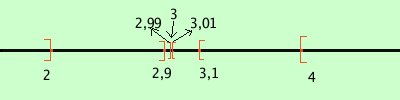
Mostriamo che i due insiemi di numeri prima classe       seconda classe      2 2,9 2,99 2,999 2,9999 2,99999 ............ 4 3,1 3,01 3,001 3,0001 3,00001 ............ formano due classi contigue di numeri razionali: sono separate ogni numero della prima classe e' piu' piccolo di 3 ogni numero della seconda classe e' piu' grande di 3 godono dell'avvicinamento indefinito scelgo un numero piccolissimo ad esempio 0,000001 (un milionesimo): posso prendere un numero nella prima classe ed un numero della seconda classe tali che la differenza sia ancora piu' piccola basta prendere due numeri con piu' di 6 cifre decimali, ad esempio prendo quelli con 7 cifre decimali 2,9999999      3,0000001 la loro diffferenza vale 3,0000001 - 2,9999999 = 0,0000002 cioe' due decimilionesimi che e' meno di un milionesimo Mostriamo che i due insiemi di numeri prima classe       seconda classe      1 1,4 1,41 1,414 1,4142 1,41421 1,414213 1,4142135 1,41421356 1,414213562 1,4142135623 ............. 2 1,5 1,42 1,415 1,4143 1,41422 1,414214 1,4142136 1,41421357 1,414213563 1,4142135624 ............ 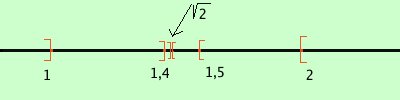formano due classi contigue di numeri razionali: sono separate ogni numero della prima classe e' piu' piccolo di 2 ogni numero della seconda clase e' piu' grande di 2 godono dell'avvicinamento indefinito scelgo un numero piccolissimo ad esempio 0,000001 (un milionesimo): posso prendere un numero nella prima classe ed un numero della seconda classe tali che la differenza sia ancora piu' piccola basta prendere due numeri con piu' di 6 cifre decimali, questa volta prendo quelli con 9 cifre decimali 1,414213562      1,414213563 la loro diffferenza vale 1,414213563 - 1,414213562 = 0,000000001 cioe' un miliardesimo che e' meno di un milionesimo