|
Facciamo ora la conoscenza di un ente che ci accompagnera' lungo tutta l'analisi matematica e la geometria cartesiana: la retta reale R In questa retta ad ogni punto corrisponde un numero reale e ad ogni numero reale corrisponde un punto. Cioe' esiste una corrispondenza biunivoca fra i punti della retta ed i numeri reali 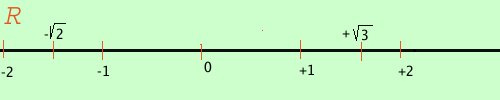
C'e' da dire che i numeri reali non razionali saranno molti di piu' dei numeri reali razionali: addirittura avremo che mentre i numeri razionali, per quanto infiniti sono un'infinita' numerabile, i numeri reali sono un'infinita' non numerabile e , siccome rappresentandoli su una retta, fra un numero e l'altro non esiste piu' spazio, si parlera' di continuo |

|

|

|

|