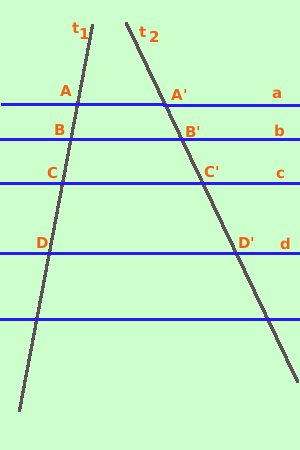
Segmenti compresi fra rette parallele tagliate da due trasversali formano due classi di grandezze proporzionali Un fascio di rette parallele e' l'insieme di tutte le rette parallele ad una retta data; naturalmente noi non possiamo disegnarle tutte, disegneremo solo quelle che ci servono, ma tu devi pensare che per ogni punto passa una delle rette del fascio Naturalmente quando parliamo di segmenti in proporzione intendiamo che le loro misure sono in proporzione So per ipotesi che le rette a, b, c, d sono parallele, devo dimostrare che i segmenti formati sulla prima retta t1 e quelli formati sulla seconda retta t2 sono fra loro proporzionali: AB : A'B' = CD : C'D'
Dividiamo la dimostrazione in due parti:
|

|

|

|

|