Teorema inverso del precedente Vale il teorema: 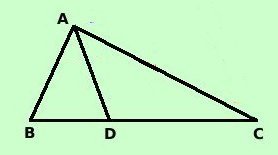Se la congiungente il vertice con un punto del lato opposto divide il lato opposto in parti proporzionali agli altri due lati allora tale congiungente e' la bisettrice dell'angolo al vertice So che vale AB : AC = BD : DC devo dimostrare che la retta AD e' la bisettrice dell'angolo BAC; Ipotesi AB : AC = BD : DC             Tesi        BAD = DAC ^ ^ Dimostrazione: Qui partiamo dalla validita' del teorema di Talete, quindi partiamo dalle parallele e cerchiamo di arrivare a mostrare che gli angoli sono uguali Siccome vale la proporzione posso riportare un segmento AE = AC sul prolungamento di BA dalla parte di A congiungo E con C Essendo valido il teorema inverso del teorema di Talete avremo che le rette AD ed EC sono fra loro parallele, e per il teorema inverso del fondamentale sul parallelismo avremo che gli angoli DAC^ ed ACE^ sono congruenti fra loro Abbiamo inoltre che il triangolo AEC e' isoscele e quindi avremo AEC = ACE ^ ^ Sappiamo che la somma degli angoli interni di un triangolo vale un angolo piatto cioe' la somma AEC + ACE + CAE^ ^ ^ e' uguale ad un angolo piatto Ma anche l'angolo BAE^=  BAD + DAC + CAE ^ ^ ^ e' uguale ad un angolo piatto ed essendo tutti gli angoli piatti congruenti avremo AEC + ACE + CAE^^^=     BAD + DAC + CAE ^ ^ ^ Possiamo eliminare l'angolo CAE^ da entrembe le parti AEC + ACE^^ =     BAD + DAC^ ^ Ma noi sappiamo che gli angoli AEC^ e ACE^ sono congruenti per costruzione, e siccome DAC^ ed ACE^ sono congruenti fra loro per il teorema inverso del fondamentale sul parallelismo ne deriva che gli angoli BAD^ e DAC^ sono congruenti, cioe' la retta AD e' la bisettrice dell'angolo BAC^ come volevamo