|
Questo e' uno dei teoremi meno usati, ma quando capita .... Insegnavo alle magistrali quando ho incontrato un esercizio (l'unico mai visto) basato sul terzo criterio e ci sono stato sopra 3 giorni prima di capire cos'era e come venirne a capo Se due triangoli hanno i tre lati ordinatamente in proporzione allora i due triangoli sono simili
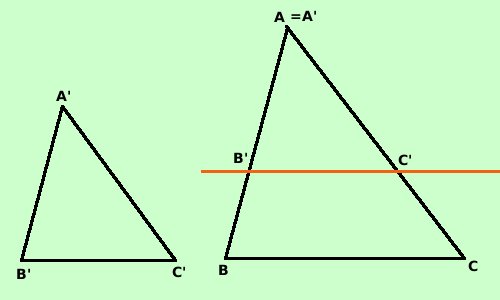 Consideriamo prima la proporzione
Consideriamo prima la proporzioneAB : A'B' = AC : A'C' Se AB = A'B' e quindi AC = A'C' (e vale anche BC = B'C') allora i due triangoli sono congruenti per il terzo criterio di congruenza e quindi i triangoli sono simili Tutti i triangoli congruenti fra loro sono simili con rapporto di similitudine uguale ad 1; possiamo dire che la relazione di congruenza e' contenuta nella relazione di similitudine nel senso che figure congruenti sono anche simili, mentre figure che sono simili generalmente non sono congruenti Se invece AB e' diverso da A'B' allora supponendo che A'B' < AB possiamo sovrapporre A'B' su AB, partendo da A ed anche A'C' su AC, sempre partendo da A. Allora per il corollario al teorema di Talete possiamo dire che B'C' e' parallelo a BC e quindi: ABC = A'B'C'^ ^ perche' angoli corrispondenti rispetto alle rette parallele B'C' e BC tagliate dalla trasversale AB BCA = B'C'A'^ ^ perche' angoli corrispondenti rispetto alle rette parallele B'C' e BC tagliate dalla trasversale AC Posso poi rifare lo stesso ragionamento relativamente alla proporzione AB : A'B' = BC : B'C' e quindi ottenere la tesi |

|

|

|

|