Area del triangolo noti perimetro e raggio del cerchio inscritto Considero un triangolo ed il suo cerchio inscritto: conosco il valore del perimetro del triangolo 2p conosco anche il valore del raggio r del cerchio inscritto Con queste condizioni posso calcolare l'area del triangolo Congiungendo il centro del cerchio con i vertici del triangolo ottengo tre triangoli che hanno come altezza il raggio. Per il teorema sull'equivalenza fra triangoli aventi stessa base e stessa altezza posso trasformare la figura in un secondo triangolo avente come base il perimetro e come altezza il raggio 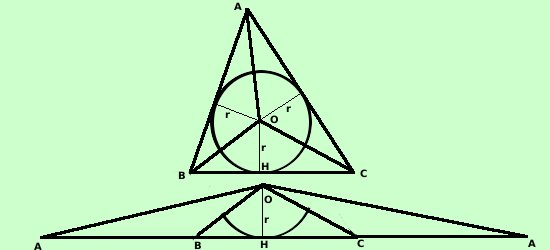ognuno dei triangolini di cui e' composta la seconda figura ha la stessa area del triangolino corrispondente nella prima figura (quelli corrispondenti hanno gli stessi vertici) Ma la seconda figura e' un triangolo che ha come base il perimetro del primo triangolo e come altezza il raggio quindi per l'area vale As(ABC) = (AB+BC+CA)·OH ------------------------- 2 2p · r = ---------   2 L'area del triangolo si ottiene moltiplicando il perimetro del triangolo per il valore del raggio del cerchio inscritto e dividendo il risultato per 2 As = 2p · r = ---------   2 Oppure piu' semplicemente, essendo p il semiperimetro L'area del triangolo si ottiene moltiplicando il semiperimetro del triangolo per il valore del raggio del cerchio inscritto As = p · r