Teorema di Tolomeo Teorema: Per ogni quadrilatero inscritto in una circonferenza la somma dei prodotti delle misure dei lati opposti e' uguale al prodotto della misura delle due diagonali 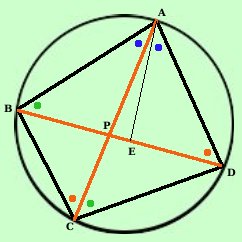Piu' difficile da dire che da applicare: vale a dire che per le misure dei segmenti vale: AB · CD + BC · AD = AC · BD Dimostrazione: Dal lato AD del quadrilatero riporto il segmento AE in modo che l'angolo EAD sia congruente all'angolo BAC Considero i due triangoli BAC e AED, essi hanno: BCA = EDA^^ perche' angoli alla circonferenza che insistono sullo stesso arco BC (se prolungo ED ....) BAC = EAD^^ per costruzione: Quindi i due triangoli BAC ed AED sono simili per il primo criterio di similitudine e posso scrivere: Te li ordino secondo gli angoli per scrivere meglio la proporzione A C B A D E AC : AD = BC : DE ed applicando la proprieta' fondamentale BC · AD = AC · DE Considero ora i triangoli ACD ed AEB, essi hanno: DAC = EAB^^ perche' somma di angoli congruenti (DAE=PAB) con lo stesso angolo EAP ABD = ACD^^ perche' angoli alla circonferenza che insistono sullo stesso arco AD Quindi i due triangoli ACD ed ABE sono simili per il primo criterio di similitudine e posso scrivere: Te li ordino secondo gli angoli per scrivere meglio la proporzione A C D A B E AC : AB = CD : BE ed applicando la proprieta' fondamentale AB · CD = AC · BE Ora riprendo entrambe i prodotti finali AB · CD = AC · BE BC · AD = AC · DE sommo termine a termine AB · CD + BC · AD = AC · BE + AC · DE raccolgo a fattor comune AC AB · CD + BC · AD = AC ·(BE + DE) ed essendo BE + DE = BD avro' AB · CD + BC · AD = AC · BD come volevamo