|
In un triedro ogni faccia e' minore della somma delle altre due Come dimostrazione e' un po' laboriosa, ma ha una discreta importanza Intuitivamente, se penso il triedro con una faccia fissa e le altre due incernierate che possano ruotare attorno al lato della faccia fissa, il teorema mi dice che, se ruoto le due facce portandole sull'angolo fisso, allora le due facce risulteranno in parte sovrapposte: e' l'equivalente nello spazio del teorema sul triangolo: in ogni triangolo un lato e' minore della somma degli altri due Per faccia intendiamo l'angolo formato da due semirette uscenti dal vertice del triedro e passanti per i vertici del triangolo generatore
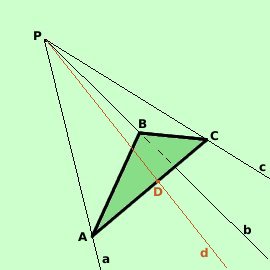Supponiamo che aPc^sia la faccia maggiore (altrimenti il teorema e'
evidente); su di essa prendiamo cPd^= cPb^Ora passiamo a costruire il triangolo di base ABC Fissiamo sulla semiretta Pa il punto A e sulla semiretta Pc il punto C Il segmento AC interseca la semiretta Pd nel punto D. Dal punto P riportiamo sulla semiretta b il segmento PD = PB. In questo modo determino il punto B ed ho costruito il triangolo ABC Considero ora i triangoli PBC e PCD; essi hanno BC = CD per costruzione CPD^= CPB^sempre per costruzione PC in comune Quindi i due triangoli sono congruenti per il primo criterio di congruenza dei triangoli Considero ora il triangolo ABC; per le proprieta' dei triangoli so che un lato e' maggiore della differenza degli altri due lati, cioe' AB > AC - BC e siccome BC = CD avro' AB > AC - CD cioe' AB > AD Considero ora i triangoli PAB e PAD; essi hanno PA in comune PB = PD per costruzione Ma i due triangoli PAB e PAD non sono congruenti ed avendo disuguali i terzi lati avranno disuguali anche gli angoli opposti a tali lati, e, in particolare APB^> APD^ sommiamo ad entrambe i membri della disuguaglianza le due quantita' uguali BPC^= DPC^ APB^+ BPC^> APD^+ DPC^ e quindi, essendo APD^+ DPC^= APC^ otteniamo APB^+ BPC^> APC^ A tali angoli di triangoli corrispondono le facce del triedro aPb^+ bPc^> aPc^ Come volevamo |
|
|
|
|