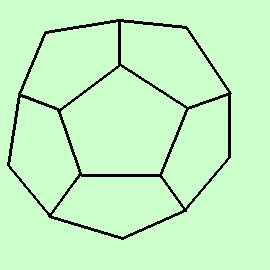
Consideriamo ora come figura base il pentagono regolare.Per il teorema sulla somma degli angoli interni di un poligono avremo che la somma degli angoli interni vale 180° x (5-2) = 180° x 3 = 540° Essendo il pentagono regolare avra' tutti e 5 gli angoli interni congruenti, quindi uno degli angoli interni vale 540° : 5 = 108° facciamo confluire tre vertici di tre pentagoni regolari congruenti in un angoloide: l'angoloide misurera' quindi 324°; Continuiamo la costruzione facendo in modo che in ogni vertice confluiscano i vertici di 3 pentagoni. In tal modo lo spazio viene racchiuso in un poliedro regolare: il Dodecaedro regolare Il dodecaedro regolare ha: 12 facce formate da pentagoni regolari congruenti 30 lati congruenti 20 angoloidi di 324° congruenti |
|
|
|
|