|
Ora dobbiamo passare a calcolare il volume di una piramide: per semplificare i calcoli premetto il principio di Cavalieri, che ci permettera' di ottenere le formule per il volume della piramide (e non solo) in modo abbastanza semplice ed intuitivo. Quando insegnavo alle magistrali preferivo sempre questo metodo a quello classico degli scaloidi (una specie di integrale spiegato ad alunni che, come programma, non avevano nemmeno le equazioni di secondo grado complete). Se a qualcuno il metodo dello scaloide interessa me lo scriva ed io lo inserisco in una nota in questa pagina 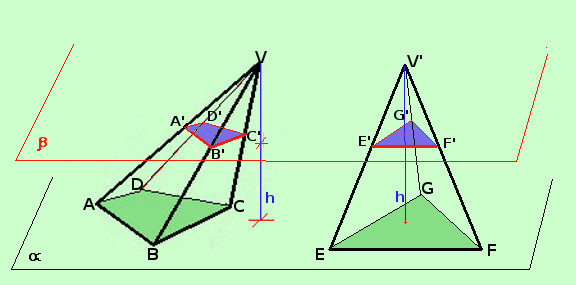
Enunciamo il principio di Cavalieri: Consideriamo due solidi aventi la stessa altezza h. Se tali solidi, aventi le basi equivalenti (stessa area) sono tagliati da piani paralleli al piano di base secondo poligoni equivalenti allora i due solidi hanno lo stesso volume Se, essendo uguale l'altezza, As(ABCD) = As(EFG) e Per ogni piano As(A'B'C'D') = As(E'F'G') allora vale Vol(VABCD) = Vol(V'EFG) Cioe', intuitivamente, se, tagliando i solidi, mi vengono sempre fette equivalenti allora i due solidi hanno lo stesso volume Come conseguenza immediata del pricipio di Cavalieri possiamo dire che due piramidi sono equiestese (cioe' hanno lo stesso volume) se hanno basi equivalenti e stessa altezza, come rappresentato in figura |

|

|

|

|