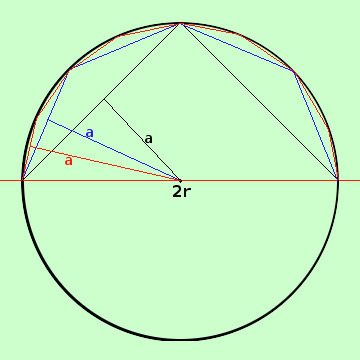
Applicazione alla superficie di una sfera Applichiamo ora quanto visto alla superficie di una sfera Consideriamo per semplicita' il quadrato inscritto nella circonferenza (la dimostrazione si potrebbe fare comunque partendo da un qualunque poligono regolare) Allora nella semicirconferenza superiore posso inscrivere mezzo quadrato con due vertici sul diametro e la sua area di rotazione sara' data da Area = 2a π (2r) consideriamo ora i punti medi sugli archi che congiungono i vertici del quadrato e consideriamo quindi il mezzo ottagono regolare inscritto nella semicirconferenza (in blu); Anche per la sua superficie di rotazione abbiamo Area = 2a π (2r) consideriamo ora i punti medi sugli archi che congiungono i vertici dell'ottagono regolare e consideriamo quindi il mezzo poligono regolare a 16 lati (in rosso); Anche per esso abbiamo che la la superficie di rotazione vale Area = 2a π (2r) Notiamo che ogni volta che prendiamo i punti medi la poligonale si avvicina alla semicirconferenza e il valore dell'apotema si avvicina al valore del raggio Quindi, considerando la semicirconferenza come la poligonale derivante dal mezzo poligono regolare con infiniti lati avremo che, essendo apotema=r vale la formula Area = 2 r π (2r) = 4 π r2 quindi Sfera Area della superficie sferica = 4 π r2 L'area della superficie di una sfera equivale a 4 volte l'area del suo cerchio massimo (cerchio massimo = uno dei cerchi della sfera contenenti il centro)