 Prima di tutto devo avere la possibilita' di calcolare una distanza AD che sia
allineata con la base della torre
Prima di tutto devo avere la possibilita' di calcolare una distanza AD che sia
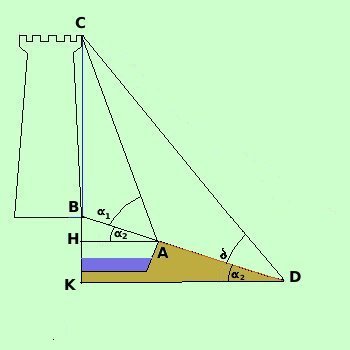
allineata con la base della torreConosciamo La distanza AD L'angolo L'angolo L'angolo Essendo i triangoli ABH e DBK simili avro' inoltre che angolo BAH = angolo BDK = Al solito possiamo misurare AD con un decametro a nastro e gli angoli mediante il teodolite se considero il triangolo ACD in esso l'angolo BAC e' un angolo esterno e quindi uguale alla somma degli angoli interni non adiacenti BAC = ADC + ACD e quindi, ricavando ACD ACD = BAC - ADC = Quindi se considero il triangolo CAD ne conosco due angoli ed un lato e quindi posso risolverlo: possiamo calcolare AC con il teorema dei seni
Se ora considero il triangolo BAH in esso l'angolo CBA e' esterno e quindi uguale alla somma degli angoli interni non adiacenti, cioe' CBA = BAH + HAB = 90° + Se quindi considero il triangolo CBA in esso conosco due angoli ed un lato: CBA = 90° + CAB =
|