|
Consideriamo la formula dell'interesse semplice I = C i t Per semplicita' considero il capitale C costituito da 1 euro, cosi' possiamo toglierlo dalla formula. Per avere poi il risultato finale per un capitale C bastera' moltiplicare quello che otteniamo per C I = i t Se cosideriamo fisso il tasso i abbiamo che l'interesse I dipende dal tempo t cioe' l'interesse e' funzione lineare del tempo (cioe' piu' tempo impiego il capitale e maggiore e' l'interesse, se raddoppio il tempo raddoppia l'interesse, se triplico il tempo triplica l'interesse,...) Esiste quindi una proporzionalita' diretta fra il tempo e l'interesse e tale proporzionaita' puo' essere rappresentata in un piano cartesiano come una retta passante per l'origine di equazione y = m x con y uguale all'interesse I x uguale al tempo t ed m (coefficiente angolare) uguale a i Quindi e' possibile rappresentare graficamente come varia l'interesse al variare del tempo e la rappresentazione grafica e' sempre data da una retta passante per l'origine Siccome il tempo non puo' andare all'indietro allora noi cosidereremo solamente il tempo positivo e quindi la semiretta che parte dall'origine quindi il grafico di I = i t e' dato da 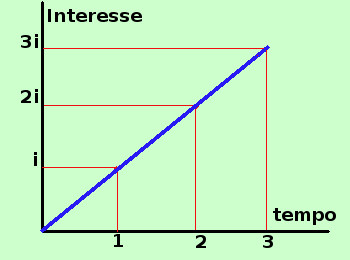 Al tempo 1 (dopo 1 anno) avremo l'interesse i (se t=1 allora I= i·1 = i) Al tempo 2 (dopo 2 anni) avremo l'interesse 2i (se t=2 allora I= i·2 = 2i) Al tempo 3 (dopo 3 anni) avremo l'interesse 3i (se t=3 allora I= i·3 = 3i) .......... Avevamo detto che l'interesse semplice viene usato per periodi inferiori all'anno e il perche' lo vedremo piu' avanti, ma per ora consideriamolo valido anche per periodi superiori all'anno Vediamo ora un esempio pratico Rappresentiamo graficamente l'interesse, sempre per un capitale di 1 euro impiegato al tasso del 2% (i = 0,02) 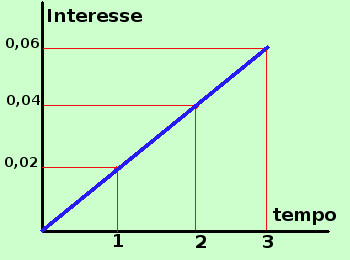 Al tempo 1 (dopo 1 anno) avremo l'interesse 0,02 cioe' 2 centesimi (se t=1 allora I= 0,02·1 = 0,02€) Al tempo 2 (dopo 2 anni) avremo l'interesse 0,04 cioe' 4 centesimi (se t=2 allora I= 0,02·2 = 0,04€) Al tempo 3 (dopo 3 anni) avremo l'interesse 0,06 cioe' 6 centesimi (se t=3 allora I= 0,02·3 = 0,06€) .......... Da notare che abbiamo usato un grafico con due scale diverse per l'orizzontale e la verticale, questo devi sempre farlo per poter evidenziare al meglio le cartteristiche del grafico che rappresenti Se il capitale e' diverso da 1 euro si procede in questo modo Rappresentiamo graficamente l'interesse, per un capitale di 1000 euro impiegato al tasso del 2% (i = 0,02) 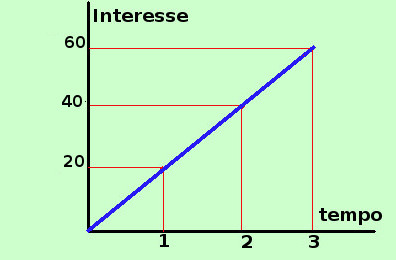 Al tempo 1 (dopo 1 anno) avremo 20 euro (se t=1 allora I= 1000·0,02·1 = 20,00€) Al tempo 2 (dopo 2 anni) avremo 40 euro (se t=2 allora I= 1000·0,02·2 = 40,00€) Al tempo 3 (dopo 3 anni) avremo 60 euro (se t=3 allora I= 1000·0,02·3 = 60,00€) .......... |

|

|

|

|