Scadenza media Troviamo ora la data scadenza media in cui devo pagare il totale delle somme dei debiti ad un tasso fisso: in tal caso la scadenza sara' sempre intermedia fra le varie scadenze considerate. da cui il nome Vediamo il metodo su un esercizio_ Devo pagare le somme di 3000 € fra 2 anni e 6000 € fra 6 anni Mi accordo con il creditore per estinguere il debito con un pagamento di € 9000; tasso fisso i= 2% In che data dovro' versare i 9000 €? Dati: debito1 = 3000   tempo1= 2 anni debito2 = 6000   tempo2= 6 anni saldo 9000 € i= 2% = 0,02 troviamo la data del versamento del saldo tx Conviene riportare tutti i dati alla data odierna ed impostare l'equazione Traccio la retta dei tempi 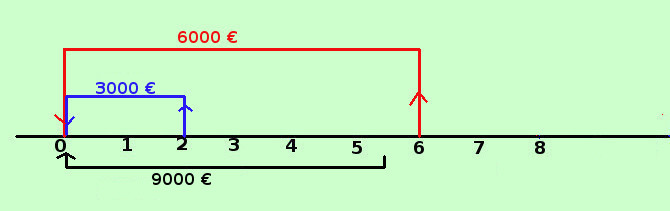Imposto l'equazione: 9000 · v-tx = 3000· 9000 · 1,02-tx = 3000· 1,02-2 + 6000 · 1,02-6 divido tutto per 1000 9 · 1,02-tx = 3· 1,02-2 + 6 · 1,02-6 1,02-tx = 3· 1,02-2 + 6 · 1,02-6 9 = leggo sulle tavole e sostituisco = 3 · 0,96116878 + 6 · 0,88797138 9 = 0,912370513 per calcolare tx passo ai logaritmi Log 1,02-tx = Log 0,912370513 -tx Log 1,02 = Log 0,912370513 tx CoLog 1,02 = Log 0,912370513 tx = Log 0,912370513 CoLog 1.02 calcolo il logaritmo al numeratore Log 0,912370513 = La caratteristica e' 1_ essendo il mio numero compreso fra 0 ed 1 Per calcolare la mantissa cerco 912370513; tale valore e' compreso fra 9123 e 9124 9123         →    96014         5 9124         →    96019    Di fianco ai due risultati trovi il numero 5 che corrisponde alla differenza fra i due valori della mantissa mentre la differenza fra il mio valore e quello minore e' 9123,705-9123 = 0,705 (approssimo alla terza cifra decimale) Nella tabella del 5 cerco i numeri 7 0 5 spostando per ogni risultato la virgola 7    → 3,5       0    → 0,00   5    → 0,025 quindi 96014        + 3,5     + 0,00   + 0,025 = 96017,525    quindi scrivo Log 0,912370513 = 1_,96017525 Calcolo il Cologaritmo al denominatore leggo sulle tavole logaritmiche a 7 decimali    CoLog 1,02 = - Log 1,02 = Essendo Log 1,02 = 0,0086002 avro' CoLog 1,02 = - Log 1,02 = -(0,0086002) = 1_9913998 Nel calcolo preferisco utilizzare quello con il meno davanti Ora posso fare la divisione e trovare tx tx = Log 0,0,912370513 CoLog 1.02 = 1_,96017525 -(0,0086002) = -1+0,9601752 -0,0086002 = -0,0398248 -0,0075344 = = 0,0398248 0,0075344 = 5,285729454 Sono 5 anni e 286 (approssimato) millesimi di anno: per vedere a quanti giorni corrispondono i decimali faccio la proporzione (uso l'anno commerciale di 360 giorni) 286:1000 = x : 360 risolvo la proporzione x = 360 · 286 1000 = 102,96 che approssimiamo a 103 giorni, cioe' 3 mesi (di 30 giorni) e 13 giorni. Quindi dovro' eseguire il pagamento di 6800 euro fra 5 anni 6 mesi e 13 giorni