Parabola che interseca in due punti l'asse delle x E' equivalente al caso ove il delta del polinomio e' maggiore di zero (2 soluzioni reali = 2 punti sull'asse x) Distinguiamo i due casi: a 0 a 0 Quando a e' minore di zero potremmo cambiare di segno tutti i termini del trinomio (cambiando anche di verso la disequazione), ma il metodo della parabola e' talmente semplice che di solito si preferisce applicarlo senza cambiare di segno 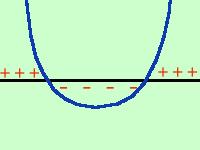a 0 Se a e' maggiore di zero la parabola ha la concavita' verso l'alto quindi avremo che il trinomio e' positivo per valori esterni all'intervallo delle intersezioni ed e' negativo per valori interni 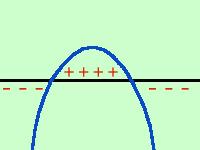0 a 0 ax 2 + bx + c 0 ax2 + bx + c 0 valori esterni all'intervallo delle radici valori interni all'intervallo delle radici a 0 Se a e' minore di zero la parabola ha la concavita' verso il basso quindi avremo che il trinomio e' positivo per valori interni all'intervallo delle intersezioni ed e' negativo per valori esterni 0 a 0 ax 2 + bx + c 0 ax2 + bx + c 0 valori interni all'intervallo delle radici valori esterni all'intervallo delle radici