Insieme Q dei numeri razionali Possiamo ora definire l'Insieme Q dei numeri razionali: Q = m/n : mZ, nZ e n 0 Si legge: Q e' l'insieme dei numeri m/n tali che m e' un numero intero, n e' un numero intero e n e' diverso da zero Se hai bisogno di aiuto per leggere la definizione Noticina storica I numeri razionali non erano noti ai babilonesi che infatti per avere meno divisioni possibili inventarono un sistema di numerazione basato sul 12 (12 e' divisibile per 2, per 3, per 4, per 6) ed e' per questo che ancor oggi abbiamo 12 mesi, 60 minuti, 60 secondi, 360 gradi (tutti multipli di 12) Invece erano noti (naturalmente senza segno) ai greci che li utilizzavano moltissimo, tra l'altro, anche per studiare musica! Una rappresentazione molto usata sara': 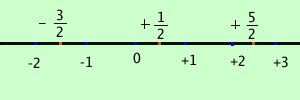la retta dei numeri razionali facendo corrispondere ad ogni numero razionale un punto della retta (3 ad esempio puo' essere pensato 3/1 e quindi razionale) Una rappresentazione mediante teoria degli insiemi potrebbe essere la seguente: Z e' un sottoinsieme dell'insieme Q quindi i numeri che si corrispondono in Z ed in Q devono avere in Q le stesse proprieta' che avevano in Z in particolare lo zero resta l'elemento neutro per l'addizione e l'elemento assorbente per la moltiplicazione mentre l'uno e' l'elemento neutro per la moltiplicazione Un po' di nomenclatura 3 --- 5 il 3 si chiama numeratore il 5 si chiama denominatore la linea tra numeratore e denominatore si chiama linea di frazione il tutto si chiama frazione dobbiamo ora definire come operare in Q equivalenza addizione sottrazione moltiplicazione divisione