|
Abbiamo ora un insieme ove vi sono numeri che, anche se scritti in modo diverso, hanno lo stesso valore come ad esempio 1/2 2/4 3/6 4/8 5/10 . . . . . Senza scomodare la retta possiamo anche rappresentarli in questo modo 
1/2 significa che prendo una cosa, la divido in due parti e ne prendo la meta' 2/4 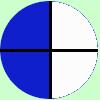
2/4 significa che prendo una cosa, la divido in quattro parti e ne considero due 3/6 
3/6 significa che prendo una cosa, la divido in sei parti e ne prendo tre 4/8 
4/8 significa che prendo una cosa, la divido in otto parti e ne considero quattro Eccetera....... Se ora ti dicessi: considera le frazioni equivalenti: 1/3 = 2/6 = 3/9 = . . . . . cosa metteresti al posto dei puntini? Scriviamo ora la regola di equivalenza fra le frazioni:
Per numero intendiamo anche frazioni: per trasformare 2/4 in 4/8 basta moltiplicare numeratore (sopra) e denominatore (sotto) per 2 per trasformare 2/4 in 5/10 bisogna moltiplicare sopra e sotto per 5/2, cioe' moltiplicare per 5 e poi dividere per 2 sia al numeratore che al denominatore 2 2·5 10 10:2 5 --- = ---- = ---- = ------- = ---- 4 4·5 20 20:2 10 Allora visto che le frazioni equivalenti hanno lo stesso valore quando scrivero' una frazione scegliero' sempre la forma piu' semplice possibile dividendo numeratore e denominatore per lo stesso numero (ricordati che in matematica si sceglie sempre la strada piu' semplice), ad esempio se ho --- 14 --- 2 |

|

|

|

|