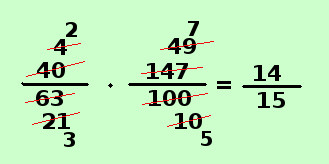Applicazione al prodotto fra numeri razionali quando fai il prodotto fra numeri razionali, se le frazioni hanno termini complicati, conviene prima di eseguire il prodotto semplificare, utilizzando i criteri di scomposizione, il primo numeratore per il secondo denominatore ed il primo denominatore per il secondo numeratore e moltiplicare successivamente le frazioni risultanti Vediamo qui direttamente un esempio su come procedere: Esempio 40 63 · 147 100 = Supponendo di avere le frazioni gia' ridotte a forma normale devo vedere se hanno fattori comuni il primo numeratore con il secondo denominatore ed il primo denominatore con il secondo numeratore (brevemente si dice in croce) 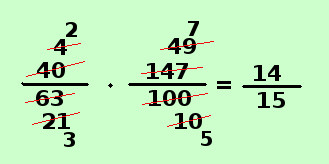Devo semplificare 40 con 100 sono entrambe semplificabili per 10, quindi ottengo 4 e 10 Questi due numeri sono ancora divisibili per 2 quindi ottengo 2 e 5 devo semplificare 63 e 147 sono entrambe semplificabili per 3 quindi ottengo 21 e 49 Questi due numeri sono divisibili per 7 (ripassa le tabelline!) quindi ottengo 3 e 7 40 63 · 147 100 = 4 21 · 49 10 = 2 3 · 7 5 = 14 15 Naturalmente quanto fatto e' il procedimento per esteso: nei compiti in classe questi calcoli si fanno a parte su un angolo di foglio e scrivendo sopra e sotto in sequenza, come vedi dall'immagine qui sopra a fianco.