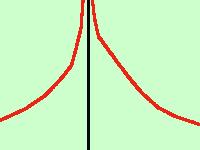
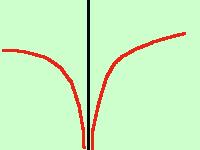
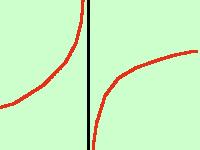
 Si ha un asintoto vericale quando, all'avvicinarsi della x ad un valore finito, il valore della y cresce
all'infinito
Si ha un asintoto vericale quando, all'avvicinarsi della x ad un valore finito, il valore della y cresce
all'infinitoPoiche' il valore infinito e' solo una convenzione ne deriva che la funzione avra' valore infinito dove la x non e' definita, cioe' per valori non appartenenti al campo di esistenza Quindi per trovare gli asintoti verticali dovremo trovare quei valori della x per cui la funzione vale infinito, cioe' supponendo che nel punto x = c la funzione non sia definita dovremo calcolare: limx->c f(x) = se il risultato vale x = c sara' l'asintoto verticale E' bene al fine di calcolare esattamente come la funzione sparisce all'infinito calcolare sia il limite destro che il limite sinistro per trovare il segno dell'infinito a destra e a sinistra dell'asintoto ricordati del teorema della permanenza del segno che ti permette di assegnare all'infinito (anche se non esiste) un segno positivo o negativo I quattro casi possibili sono rappresentati qui sotto:
Facciamo un esercizio semplicissimo: vediamo se la funzione 3x y = ------- x - 1 ha asintoti verticali il campo di esistenza e' tutti i valori eccetto x = 1 per cui si annulla il denominatore calcolo: 3x limx->1 -------- = 3/0 = x - 1 quindi la retta x = 1 e' un asintoto verticale Per tracciarlo al meglio calcoliamo i limiti destro e sinistro della funzione nel punto 1
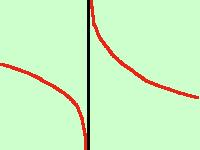 limx->1- f(x) = - |

|

|

|

|