|
E' il caso classico: in questo caso le due circonferenze di base hanno due punti comuni fra loro. Vediamo un esercizio completo Dato il fascio di circonferenze: (1+k)x2 + (1+k)y2 + 4(1-2k)x + 2(k-1)y -4(5+7k) = 0 trovare i punti base del fascio e controllare che la retta dei centri e' perpendicolare all'asse radicale delle due circonferenze Prima separiamo i termini contenenti il parametro da queli non contenenti il parametro x2 + kx2 + y2 +ky2 + 4x -8kx + 2ky -2y -20 -28k = 0 x2 + y2 + 4x -2y -20 + k(x2 + y2 -8x + 2y -28) = 0 Abbiamo quindi le due circonferenze di base
Calcolo l'asse radicale sottraendo fra loro le due equazioni membro a membro x2 + y2 + 4x -2y -20 =0 x2 + y2 -8x + 2y -28 = 0 12x -4y + 8 = 0 Posso dividere per 4 ed ottengo l'equazione dell'asse radicale 3x -y + 2 = 0 Quindi, per trovare i punti comuni (punti base del fascio) risolvo il sistema x2 + y2 + 4x -2y -20 =0 Calcoli e trovo come risultato A(-2;-4) B(1;5) Troviamo ora i centri delle due circonferenze e, quindi, la retta dei centri
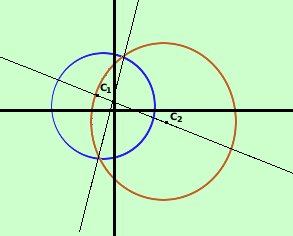
2x + 6y -2 = 0 divido per 2 x + 3y -1 = 0 la pongo in forma esplicita y = -1/3 x + 1/3 la confronto con la forma esplicita dell'asse radicale y = 3x + 2 essendo i coefficienti angolari -1/3 e 3 uno inverso ed opposto dell'altro le due rette sono perpendicolari fra loro come dovevamo verificare |

|

|

|

|