|
Se consideriamo due parabole qualunque della famiglia e ne facciamo l'intersezione, e troviamo le coordinate di due punti, questi saranno chiamati punti base della famiglia. Teoricamente, per trovare i punti base di una famiglia di parabole partiamo dall'equazione:dividiamo i termini contenenti la k da quelli senza k e scriviamo y= a'x2 + b'x +c' +k(a"x2 + b"x +c") consideriamo il polinomio che e' moltiplicato per k e poniamolo uguale a zero a"x2 + b"x +c"=0 Otteniamo un'equazione di secondo grado le cui soluzioni sono le ascisse dei punti base del fascio e sostituendo tali valori nell'equazione della famiglia troviamo le ordinate corrispondenti Infatti sostituendo il valore delle x trovate nell'equazione della famiglia le ordinate corrispondenti non dipendono piu' dal valore di k perche' i valori trovati annullano il secondo polinomio e quindi i punti trovati appartengono ad ogni parabola della famiglia indipendentemente dal valore di k Data la famiglia di parabole di equazione y = (1-k)x2 - kx + 2k - 4 trovarne le coordinate dei punti base Voglio suddividere i termini con la k da quelli senza la k: eseguo la moltiplicazione y = x2 - kx2 - kx + 2k - 4 separo i termini con la k da quelli senza la k y = x2 - 4 - kx2 - kx + 2k raccolgo la k y = x2 - 4 + k(-x2 - x + 2) pongo -x2 - x + 2 = 0 essendo uguale a zero posso cambiare di segno tutti i termini x2 + x - 2 = 0 risolvo ed ottengo x1= -2 x2= 1 ora sostituisco tali valori nell'equazione della famiglia: il secondo polinomio si annulla y1 = (-2)2 - 4 + k(0) = +4-4 = 0 y2 = (1)2 -4 + k(0) = 1-4 = -3 quindi i punti base del fascio sono 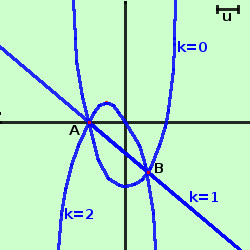
Due parabole possono avere in comune 2 punti, od uno solo oppure nessuno quindi non sempre potremo trovare i punti base Qui di fianco un grafico (molto approssimato) con i punti base A≡(-2;0) B≡(1;-3) e con alcune parabole: la parabola degenere, cioe' la retta y=-x-1 la parabola per k=0 y = x2 - 4 la parabola per k=2 (valore preso a caso come esempio) y = (1-2)x2 - (2)x + 2(2) - 4 cioe' y = -x2 - 2x |

|

|

|

|