|
Per procedere abbiamo bisogno di un concetto piu' semplice di equiestensione 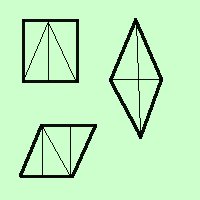 Notiamo che alcune figure si possono scomporre in "pezzi" uguali; se riusciamo a scomporre due figure in pezzi uguali potremo dire che le due figure sono equiscomponibili e quindi anche equiestese
Notiamo che alcune figure si possono scomporre in "pezzi" uguali; se riusciamo a scomporre due figure in pezzi uguali potremo dire che le due figure sono equiscomponibili e quindi anche equiesteseDefiniamo equiscomponibili due figure che possano essere scomposte in parti congruenti a destra hai l'esempio di 3 figure equiscomposte (si dice anche equicomposte) Al solito: equiscomposte se dai la precedenza alle figure equicomposte se vuoi mettere in evidenza le parti componenti |

|

|

|

|