|
Come prima cosa mostriamo che: Tutti i parallelogrammi aventi congruenti la base e l'altezza sono equiscomponibili 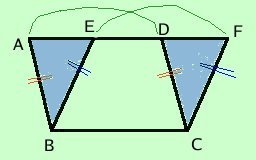 Sovrapponiamo le basi e, siccome hanno la stessa altezza, i lati opposti alle basi giaceranno sulla stessa retta. Considero i triangoli AEB e DFC essi hanno:
Infatti se considero il quadrilatero EBCD, se vi aggiungo il triangolo ABE ottengo il parallelogramma ABCD, se invece vi aggiungo il triangolo DCF ottengo il parallelogramma EBCF 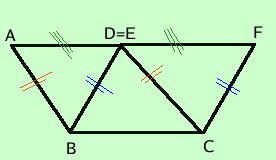 Intanto possiamo vedere alcune generalizzazioni:
Intanto possiamo vedere alcune generalizzazioni:
i due parallelogrammi hanno i lati opposti alla base con l'estremo in comune: in tal caso e' anche piu' semplice dimostrare che i due triangoli ABD ed ECF sono congruenti 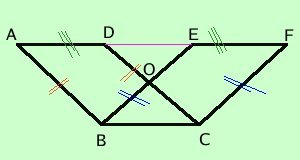 i due parallelogrammi hanno i lati opposti alla bese senza punti in comune: in tal caso prima devi dimostrare la congruenza dei triangoli ABE e CDF e poi togliere da entrambe la parte comune DOF 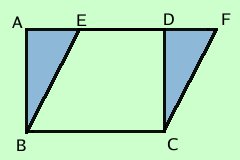 Come conseguenza notevole possiamo dire che ogni parallelogramma e' equivalente ad un rettangolo che abbia la stessa base e la stessa altezza |

|

|

|

|