|
E' forse il teorema piu' noto della geometria ma non e' quello originale di Pitagora 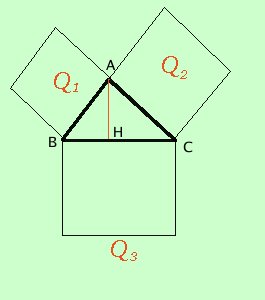 In ogni triangolo rettangolo la somma dei quadrati costruiti sui cateti e' equivalente al quadrato costruito sull'ipotenusa Cioe' Q1 + Q2 equivalente a Q3 Nei problemi sara' particolarmente importante la seguente forma del teorema Passiamo alla dimostrazione
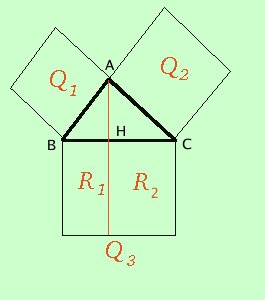 Prolungo l'altezza AH, in tal modo il quadrato Q3 venga suddiviso nei rettangoli R1 e R2 Per il primo teorema di Euclide Q1 e' equivalente a R1 per il primo teorema di Euclide Q2 e' equivalente a R2 quindi Q1 + Q2 equivalente a R1 + R2 = Q3 come volevamo In lettere scriveremo
|

|

|

|

|