 In ogni triangolo rettangolo il quadrato costruito sull'altezza relativa all'ipotenusa e' equivalente al rettangolo che ha per lati le proiezioni dei cateti sull'ipotenusa
In ogni triangolo rettangolo il quadrato costruito sull'altezza relativa all'ipotenusa e' equivalente al rettangolo che ha per lati le proiezioni dei cateti sull'ipotenusa
Nei problemi sara' particolarmente importante la seguente forma del teorema Passiamo alla dimostrazione
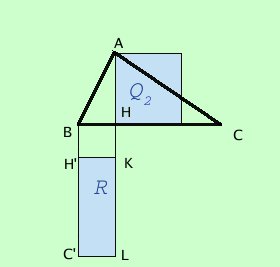
In questo teorema la cosa piu' difficile e' fare la figura come si costruisce la figura: costruisco il quadrato sul lato AB; costruisco il quadrato sull'altezza AH siccome mi serve il rettangolo di lati BH ed HC considero il rettangolo di lati BH e BC (come nella figura del primo teorema di Euclide) e poi tolgo il quadrato di lato BH 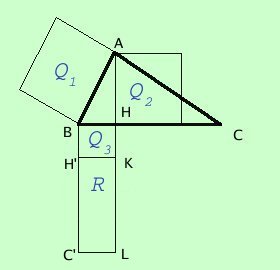 Per il primo teorema di Euclide ho che Q1 equivalente Q3 + R Per il teorema di Pitagora ho che Q1 equivalente a Q2 + Q3 per la proprieta' transitiva dell'equivalenza avro' Q3 + R equivalente Q2 + Q3 Togliendo Q3 da entrame le parti dell'equivalenza otteniamo R equivalente a Q2 come volevamo dimostrare In lettere scriveremo
|

|

|

|

|