Definizione di poligoni simili Definizione: Due poligoni sono simili se hanno tutti gli angoli uguali ed i lati corrispondenti in proporzione Se il rapporto di similitudine vale 1 allora i due poligoni, oltre che simili, sono anche congruenti Secondo me migliore e' la definizione: Se congiungendo i vertici corrispondenti di due poligoni tutte le congiungenti si intersecano in un unico punto allora i due poligoni sono simili; 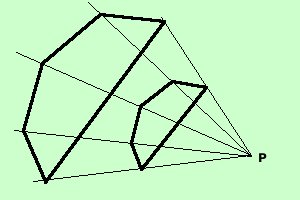Per la corrispondenza si preferisce parlare di omotetia (fare link) Se i due poligoni sono congruenti allora il punto di intersezione e' all'infinito e le rette sono parallele Siccome e' piuttosto complicato considerare tutti i lati e gli angoli, anche qui si potra' parlare di criteri di similitudine, ma, operativamente, useremo un metodo piu' intuitivo: Due poligoni sono simili se e' possibile suddividerli in triangoli ordinatamente simili Basta che consideri due vertici in corrispondenza e, da essi, tracci le congiungenti agli altri vertici: tutti i triangoli ottenuti sono tra loro simili. Puoi comunque considerare anche un punto interno al poligono ed il suo corrispondente nel secondo poligono e da questo tracciare tutte le congiungenti i vertici ed ottenere ancora triangoli simili: il problema e' trovare due punti corrispondenti nei due poligoni: se usi la seconda definizione due punti si corrisponderanno nella similitudine se sono allineati con il centro dell'omotetia (cioe' il punto in cui si incriociano tutte le congiungenti i vertici)