|
Vale il teorema: In poligoni simili le altezze stanno tra loro come i lati corrispondenti Cioe' se, ad esempio i due triangoli 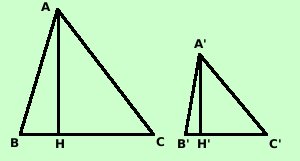 sono simili allora posso scrivere anche AB : A'B' = AC : A'C' = BC : B'C' = AH : A'H' Dimostriamolo So che i triangoli ABC ed A'B'C' sono simili allora sono simili anche i triangoli ABH ed A'B'H' infatti avremo che gli angoli ABH ed A'B'H' sono congruenti perche' angoli corrispondenti di triangoli simili gli angoli BHA e B'H'A' sono congruenti perche' retti Quindi per il primo criterio di similitudine i due triangoli sono simili e posso scrivere la proporzione BH : B'H' = AH : A'H' ma sono simili anche i triangoli AHC ed A'H'C' infatti avremo che gli angoli HCA ed H'C'A' sono congruenti perche' angoli corrispondenti di triangoli simili gli angoli AHC e A'H'C' sono congruenti perche' retti Quindi per il primo criterio di similitudine i due triangoli sono simili e posso scrivere la proporzione HC : H'C' = AH : A'H' Sommando due proporzioni valide (con lo stesso rapporto di proporzionalita') ottengo ancora una proporzione valida (BH+HC) : (B'H'+H'C') = (AH+AH) : (A'H'+A'H') BC : B'C' = 2 AH : 2 A'H' Dopo l'uguale ho una frazione e questa non cambia il suo valore se divido numeratore e denominatore per lo stesso numero; divido quindi per 2 BC : B'C' = AH : A'H' Come volevamo Si puo' dimostrare in modo piu' semplice utilizzando AB ed A'B' senza fare la somma: prova a farlo per esercizio |

|

|

|

|