Proporzionalita' fra aree Vale il teorema: In poligoni simili le aree stanno tra loro come i quadrati dei rispettivi lati Cioe' se i due pentagoni sono simili allora posso scrivere anche Area (ABCDE) : Area(A'B'C'D'E') = (AB)2 : (A'B')2 Dimostrazione 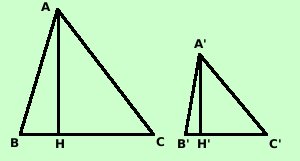Per semplicita' facciamo la dimostrazione su un triangolo, poi dividendo un qualunque poligono in triangoli potremo esportare la proprieta' a tutti i poligoni Essendo i triangoli simili posso scrivere la proporzione con le altezze (vedi pagina precedente) AB : A'B' = AH : A'H' Posso scrivere anche la proporzione (sempre valida) AB : A'B' = AB : A'B' Essendo le due proporzioni valide sara' valido anche il loro prodotto termine e termine (AB·AB) : (A'B'·A'B') = (AB·AH) : (A'B'·A'H') quindi, essendo AB·AH la doppia area di ABC e A'B'·A'H' la doppia area di A'B'C' avremo (AB)2 : (A'B')2 = 2 Area(ABC) : 2 Area(A'B'C') Dopo l'uguale ho una frazione e questa non cambia il suo valore se divido numeratore e denominatore per lo stesso numero; divido quindi per 2 (AB)2 : (A'B')2 = Area(ABC) : Area(A'B'C') Come volevamo