cos ( - ) Consideriamo un cerchio trigonometrico. Consideriamo l'angolo α nel terzo quadrante e l'angolo β nel secondo quadrante tali che la loro differenza, (α - β), sia un angolo del primo quadrante. 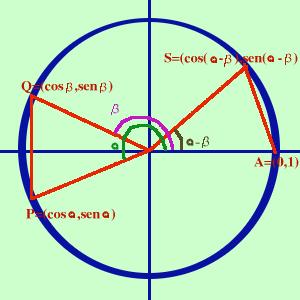Il punto P sia il punto sulla circonferenza che corrisponde ad α, Q il punto che corrisponde a β e S il punto che corrisponde ad (α - β); inoltre sia A l'origine degli archi; le coordinate cartesiane di tali punti saranno: P=(cos α , sen α ) Q=(cos β , sen β ) S=( cos( α - β ) , sen( α - β ) ) A=( 1,0 ) L'arco PQ sara'uguale all'arco AS perche' gli angoli al centro sono entrambe uguali ad (α - β) quindi avremo che anche per le corde PQ = AS applicando la formula per la distanza fra due punti nel piano per calcolare sia PQ che AS avremo PQ = [(cos α - cos β )2 + (sen α - sen β )2] AS =( [cos ( α - β ) - 1]2 + [sen ( α - β ) - 0]2) il -0 potevo tralasciarlo uguaglio le due espressioni √[(cos α -cos β )2 + (sen α - sen β )2] = √{( [cos ( α - β )] - 1)2 + [sen ( α - β )] 2} Eseguiamo i calcoli: io faccio tutti i passaggi, tu puoi abbreviare tolgo le radici prima e dopo l'uguale (cos α -cos β )2 + (sen α - sen β )2 = ( [cos α - β ] - 1)2 + [sen α - β )]2 Eseguo i quadrati cos2 α + cos 2 β -2cos α cos β + sen2 α + sen2 β -2 sen α sen β = = cos2 (α - β) + 1 - 2 cos (α - β) + sen2 (α - β) Per la prima relazione fondamentale so che cos2(angolo) + sen2(angolo) = 1 , quindi 1 + 1 -2cos α cos β -2 sen α sen β = 1 + 1 - 2 cos (α - β) gli 1 si eliminano essendo di segno uguale da parti opposte dell'uguale -2 cos α cos β -2 sen α sen β = - 2 cos (α - β) sposto i termini dalla parte dell'uguale dove sono positivi 2 cos (α - β) = 2 cos α cos β + 2 sen α sen β divido tutto per 2 ed ottengo la prima formula cos (α - β) = cos α cos β + sen α sen β La dimostrazione e' piuttosto pesante, pero' e' l'unica forma che si basa su una dimostrazione geometrica: le altre dimostrazioni saranno tutte algebriche e molto piu' semplici