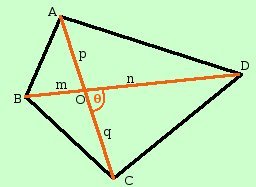
Chiamiamo O l'intersezione delle due diagonali e poniamo AC __ = d1 BD __ = d2 Poniamo inoltre AO __ = p OC __ = q BO __ = m OD __ = n BOA ^ = COD ^ = AOD ^ = BOC ^ = 180° - Per trovare l'area totale facciamo la somma delle areee dei vari triangoli componenti il quadrilatero As(ABCD) = As(AOB) + As(BOC) +As(COD) + As(DOA) Utilizziamo per trovare l'area dei triangoli la formula trovata all'inizio del capitolo As(ABCD) = =1/2pm sen Ricordando che sen (180° - As(ABCD) = 1/2pm sen Prima metto in evidenza i fattori comuni As(ABCD) = 1/2 sen Dentro parentesi posso raccogliere a fattor comune parziale = 1/2 sen = 1/2 sen Essendo p + q = d1 e m + n = d2 otteniamo la formula finale As(ABCD) = 1/2 d1 d2 sen Cioe'
|

|

|

|

|