Relazione simmetrica Diciamo che una relazione R e' simmetrica se come sottoinsieme del prodotto cartesiano AxA e' formata da un insieme simmetrico rispetto alla diagonale principale cioe' ribaltando attorno alla diagonale principale la parte sopra la diagonale si ottiene la parte sotto la diagonale esempio: 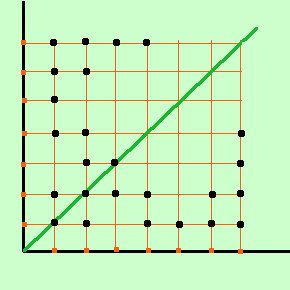In verde la diagonale principale; in nero gli elementi della relazione simmetrica diciamo che la relazione R su AxA e' simmetrica se ogni volta che si ha aRb si ha anche bRa aRb => bRa a in relazione con b implica b in relazione con a vediamone qualche esempio: Considero l'insieme degli abitanti dell'Italia e considero la relazione "abita nella stessa citta'" la relazione e' simmetrica: infatti se Maria abita nella stessa citta' di Carlo anche Carlo abita nella stessa citta' di Maria Considero gli alunni di una scuola e considero la relazione "e' nato nello stesso anno di" Per ogni alunno la relazione e' simmetrica: infatti se Antonio e' nato nello stesso anno di Cleopatra anche Cleopatra e' nata nello stesso anno di Antonio Considero gli alunni di una scuola e considero la relazione "e' piu' alto di" La relazione non e' simmetrica perche' perche' se Dante e' piu' alto di Beatrice non segue che Beatrice e' piu' alta di Dante Considero una famiglia e la relazione "e' fratello di" la relazione e' simmetrica: se Enrico e' fratello di Nicola allora anche Nicola e' fratello di Enrico