.

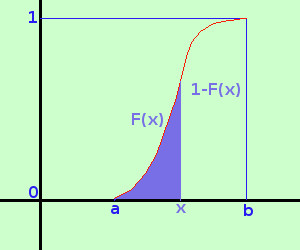
Densita' media Sia X una variabile casuale continua che assuma tutti i valori reali compresi nell'intervallo [a;b] Sia F(x) una funzione che indica che la variabile casuale assume valori inferiori od uguali ad x (in pratica una funzione che equivalga ad una parte della funzione di ripartizione partendo da sinistra: Nella funzione a fianco e' la parte colorata in azzurro) F(x) = Pr(X ≤ x) Con questa definizione avremo allora che 1-F(x) e' la probabilita'contraria, cioe' la probabilita' che la variabile casuale X assuma un valore maggiore di x cioe' quello che resta togliendo la parte azzurra 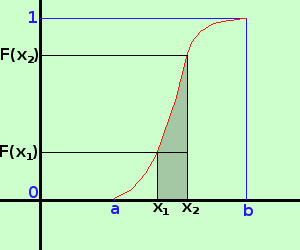F(x1) e' la probabilita'che la variabile casuale assuma un valore minore od uguale ad x1 F(x2) e' la probabilita'che la variabile casuale assuma un valore minore od uguale ad x2 F(x2)-F(x1) variazione della funzione di ripartizione e' la probabilita'che la variabile casuale assuma un valore compreso tra x1 ed x2 con x1 escluso x1<x≤x2 Nella figura a fianco la parte colorata in grigio Come ti starai rendendo conto cerchiamo di metterci nell'ottica del concetto di derivata Adesso definiamo la densita' media di probabilita' come il rapporto fra F(x2)-F(x1) ed x2 - x1, cioe' la variazione della F(x) rispetto alla variazione della x Densita' media di probabilita' F(x2)-F(x1) =    x2 - x1 Questo indica come la probabilita' si distribuisce nell'intervallo considerato nell'ipotesi che la distribuzione avvenga in modo uniforme (senza salti). Naturalmente, per poter essere un'indicazione significativa dovremo considerare un intervallo abbastanza piccolo [x; x + Δx] in tal modo otterremo la velocita' di variazione della F(x) al variare della x (velocita' all'istante) Densita' media di probabilita' F(x + Δx) - F(x) =    Δx Da notare che e' lo stesso ragionamento che si fa in fisica per calcolare la velocita' media, la velocita' istantanea e quindi la velocita' come funzione derivata dello spazio rispetto al tempo