Montante sulla retta dei tempi Partiamo da un esempio banale: consideriamo la somma di 100 euro al tasso del 10% per un certo numero di anni, ad esempio 4, vediamo da 0 a 4 anni cosa succede Se vuoi vedere come ho calcolato 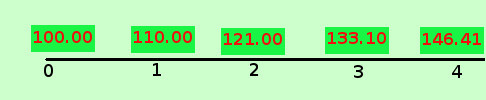Anni Valore 0 100,00 1 110,00 2 121,00 3 133,10 4 146,41 In pratica il capitale si trasforma, man mano che passa il tempo, assumendo un nuovo valore dipendete dal tasso di interesse Ma quello che dobbiamo tenere ben presente e' che possiamo pensare il valore del capitale sempre equivalente a se' stesso, solo che il tempo scorre e quindi lo trasforma, ma il suo valore effettivo intrinseco non varia E' come per l'inflazione: se ho un inflazione al 10% quello che compro ora con 100 euro il prossimo anno lo comprero' con 110 euro, fra due anni con 121 euro eccetera....quindi 100 euro di oggi sono equivalenti a 121 euro fra due anni (e quindi sempre al tasso del 10% per noi sara' indifferente parlare di 100 euro ora oppure di 121 euro fra due anni) Quindi, per quanto visto sopra, considerando la formula del montante per un certo numero n di anni Mn = C(1+i)n possiamo pensare che il fattore (1+i)n sposti in avanti il capitale nel tempo, mantenedolo equivalente a se' stesso Visto l'importanza dell'argomento, attribuiamo un simbolo speciale a tale fattore (1+i)n = un Quindi un sara' il fattore che mi sposta in avanti il capitale nel tempo di n anni