Valore attuale sulla retta dei tempi Lo stesso ragionamento che abbiamo fatto per il montante possiamo fare anche per lo sconto Partiamo anche qui da un esempio banale: consideriamo la somma di 146,41 euro (ho preso la somma della pagina precedente) al tasso del 10% che devo pagare fra 4 anni, vadiamo da 0 a 4 anni cosa succede se pago prima Se vuoi vedere come ho calcolato 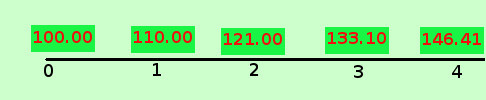Anni Valore scontato 4 146,41 3 133,10 2 121,00 1 110,00 0 100,00 In pratica il valore attuale si trasforma, man mano che indietreggiamo nel tempo, assumendo un nuovo valore dipendete dal tasso di interesse Anche qui, quello che dobbiamo tenere ben presente e' che possiamo pensare il valore del capitale sempre equivalente a se' stesso, solo che il tempo scorre e quindi lo trasforma, ma il suo valore effettivo intrinseco non varia Cioe' al tasso del 10% la somma di euro 146,41 fra 4 anni e' equivalente alla somma di euro 100,00 ora od anche al tasso del 10% quello che comprero' fra 4 anni con euro 146,41 adesso posso acquistarlo con euro 100 Quindi, per quanto visto sopra, considerando la formula del valore attuale per lo sconto composto per un certo numero n di anni V = C (1+i)n possiamo pensare che il fattore 1/(1+i)n sposti indietro il capitale nel tempo, mantenendolo equivalente a se' stesso Visto l'importanza dell'argomento, attribuiamo un simbolo speciale a tale fattore 1 (1+i)n = vn Quindi vn sara' il fattore che mi sposta indietro il capitale nel tempo di n anni