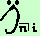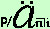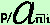Nomenclatura sui tipi di rendita Approfondimento sull'utilizzo dei simboli Per quanto riguarda le rate, supponendo le rate costanti di 1 euro, distinguendo fra montante e valore attuale avremo: Per quanto riguarda il montante se la rata scade all'inizio dei periodi in cui e' suddivisa la rendita parleremo di rendita anticipata ed utilizzeremo per indicarla il simbolo 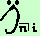si legge s anticipato figurato n al tasso i se la rata scade alla fine dei periodi in cui e' suddivisa la rendita parleremo di rendita posticipata ed utilizzeremo per indicarla il simbolo si legge s figurato n al tasso i             Per quanto riguarda il valore attuale se il primo periodo della rendita decorre da oggi parleremo di rendita immediata se la rata scade all'inizio dei periodi in cui e' suddivisa la rendita parleremo di rendita immediata anticipata ed utilizzeremo per indicarla il simbolo si legge a anticipato figurato n al tasso i      se la rata scade alla fine dei periodi in cui e' suddivisa la rendita parleremo di rendita immediata posticipata ed utilizzeremo per indicarla il simbolo si legge a figurato n al tasso i                    se il primo periodo della rendita e' situato in un anno futuro parleremo di rendita differita se la rata scade all'inizio dei periodi in cui e' suddivisa la rendita parleremo di rendita differita anticipata ed utilizzeremo per indicarla il simbolo 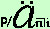si legge a anticipato differito p figurato n al tasso i se la rata scade alla fine dei periodi in cui e' suddivisa la rendita parleremo di rendita differita posticipata ed utilizzeremo per indicarla il simbolo 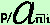si legge a differito p figurato n al tasso i             Se vuoi vedere una tabella riassuntiva dei vari casi indicati E' possibile, con un semplice accorgimento, trasformare un montante di una rendita posticipata in montante di una rendita anticipata ed anche trasformare il valore attuale di un rendita immediata anticipata nel valore attuale di una rendita immediata posticipata vediamo come fare