Caso del polinomio scomponibile con termini frazionari Quando cerchiamo i possibili divisori puo' succedere che troviamo dei valori frazionari ad esempio proviamo a scomporre: 6x2-5x +1 Trovo i divisori di Ruffini i divisori del termine noto sono +1, - 1 i divisori del primo coefficiente sono +1, -1, +2, -2, +3, -3 +6, -6 I divisori possibili li ottengo facendo i divisori del termine noto fratto i divisori del primo coefficiente, quindi ottengo +1, -1, +1/2, -1/2, +1/3, -1/3, +1/6, -1/6 (x-1); P(1) = 6(1)2-5(1)+1 = 6-5+1 0 (x+1); P(-1) = 6(-1)2-5(-1)+1 = 6+5+1 0 (x-1/2); P(1/2) = 6(1/2)2-5(1/2)+1 = 6/4-5/2+1 =      6 - 10 + 4 = ------------- = 0           4 quindi (x-1/2) e' un divisore, 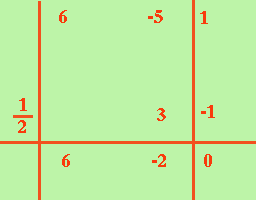quindi 6x2-5x +1=(x-1/2)(6x-2) siccome 2 diviso 6 fa 1/3 potrei anche scrivere raccogliendo 6 6x2-5x +1=6(x-1/2)(x-1/3) o meglio ancora dividendo il 6 in 2·3 e moltiplicando il primo fattore per 2 ed il secondo per 3 in modo da non avere frazioni 6x2-5x +1=(2x-1)(3x-1) Per esercizio prova a scomporre 20x3- 4x2 - 5x + 1 =